多角形化行列とTR-797改 - A Plane On The Sand

[人力飛行機設計]ご無沙汰しております。yuukivelです。

SSSで遺伝的アルゴリズムを用いた翼型設計について講演をすることになりました。
これからこのブログでも書きますが、私の翼型設計に関する知識の今のところ集大成になります。

閑話休題。本題に行きましょうか。

さて、表題の通り、今回は多角形化行列（勝手に命名）について解説する。この行列を作成することによって、多くのチームで行われている、循環分布の線形化を、行列演算だけで実現できるだけでなく、たとえば以前私が紹介した論文(TR-797,"非平面翼の最適設計-揚力と翼根曲げモーメントを与えた時の最小誘導抵抗-"）の誘導抗力最小化の演算を、多角形の循環分布で行うことができる。

つまり、こういうなめらかな循環分布ではなく…

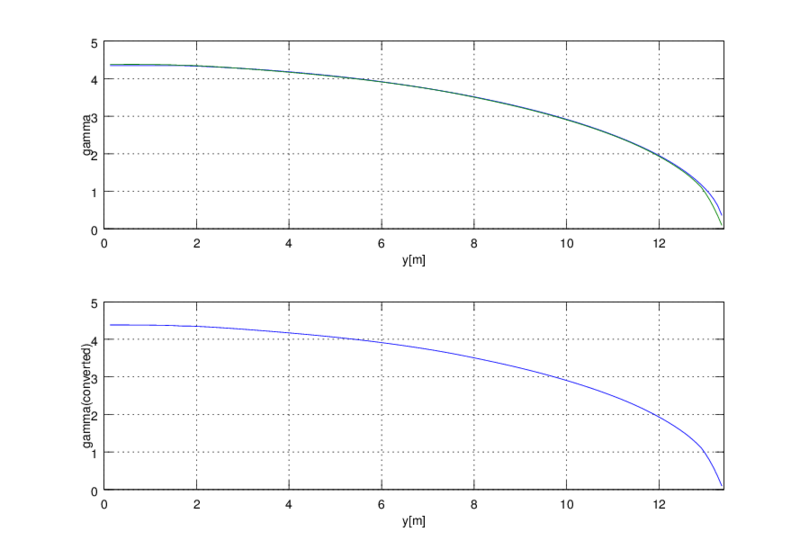
下の図の上のようなカクカクした循環分布で、誘導抗力最小となる循環分布を求めてやろうということ。青が最大たわみ2.5mの構造制約（別の記事で詳しく述べます。 $\beta$ は使いません）　赤が構造制約無し。（ついでに下のグラフは誘導角度（青)と誘導速度の最小二乗法による多角形フィッティング(赤))

循環分布を多角形化すると何がいいか、っていうと、いろいろなものが線形化できること。
1つは捻り下げや翼型変化といった主翼空力の根幹を担う値を線形化することで、解析の時間を短縮したり、解析の精度を上げたりできる。
加えて、実際に飛行機を作ったときに、リブとリブの間のプランクやストリンガーは基本的には線形補完となる。つまり、製作の際にも設計再現性の向上を図ることができる。

いままで、私の知る限りでは、「楕円循環を作る」→「テーパー変化点を探す」→「点と点を直線で結ぶ」という、何というか、スマートじゃない方法で多角形化が行われてきたように思う。

そこで今回は、もっとスマートにやりましょう。

-多角形化行列の作り方
多角形化行列POLは、区切り位置の値ベクトル $\Gamma_{ysec}$ に左からかけることで、各翼素の値に”展開”される。すなわち
$\Gamma_y=POL*\Gamma_{ysec}$
ただし、 $\Gamma_y$ は各翼素の循環の値である。

基本となる式は、線形補完の式
$\Gamma_y=(\Gamma_{ysec2}-\Gamma_{ysec1})/(ysec2-ysec1)*(y-ysec1)+\Gamma_{y1}$ 　
による。ysec1は多角形化の区切りの位置を意味する。

この式を $\Gamma_{ysec1}$ と $\Gamma_{ysec2}$ に関する項に分ける。
[tex:\Gamma_y=(-(y-ysec2)/(ysec2-ysec1))*\Gamma_{ysec1}+*1*\Gamma_{ysec2}]

こんな感じで行列表記すると
$\begin{bmatrix} \Gamma_y1 \\ \Gamma_y2 \\ \Gamma_y3 \\ \Gamma_y4 \\ \Gamma_y5 \\ \Gamma_y6 \end{bmatrix}=\begin{bmatrix} -(y1-ysec2)/(ysec2-ysec1)&(y1-ysec1)/(ysec2-ysec1)&0 \\ -(y2-ysec2)/(ysec2-ysec1)&(y2-ysec1)/(ysec2-ysec1)&0 \\ -(y3-ysec2)/(ysec2-ysec1)&(y3-ysec1)/(ysec2-ysec1)&0 \\ -(y4-ysec2)/(ysec2-ysec1)&(y4-ysec1)/(ysec2-ysec1)&0 \\ 0&-(y5-ysec3)/(ysec3-ysec2)&(y5-ysec2)/(ysec3-ysec2) \\ 0&-(y6-ysec3)/(ysec3-ysec2)&(y6-ysec2)/(ysec3-ysec2) \end{bmatrix}*\begin{bmatrix} \Gamma_ysec1 \\ \Gamma_ysec2 \\ \Gamma_ysec3 \end{bmatrix}$

おわかり戴けただろうか。上の例ではy4とy5の間にセクションの切れ目がある。つまり、ここでカクッと曲がる。
これを私は勝手に多角形化行列と名付けた。

octaveで書いた多角形化行列の作り方を載せておく。num_sectionはセクションの総数を表し、yはそのままy座標、Ndiv_secはセクションの切れ目のy座標が変数yの何行目とするかを示している。

%-----循環分布多角形化行列
for i=1:Ndiv_sec(1)
	pol_g(i,1)=1;
	pol_g(i,num_section)=0;
end

for j=2:num_section
	for i=Ndiv_sec(j-1)+1:Ndiv_sec(j)
		pol_g(i,j-1)=(-(y(i)-y_section(j))/(y_section(j)-y_section(j-1)));
		pol_g(i,j)=((y(i)-y_section(j-1))/(y_section(j)-y_section(j-1)));
	end
end

-多角形化行列の応用
例として、先に書いたとおり多角形化行列を用いてTR797を改良する。
TR797の中には、ラグランジュの未定乗数法を用いて最小誘導抗力を求めるのに、
評価関数
$H({g};\mu_1 \mu_2)={g}^{T}*{A}*{g}-\mu_1*({c}^{T}*{g}-1)-\mu_2*({b}^{T}*{g}-\beta)$
の極値を求める。このとき、解を求めるのに逆行列問題
$A*{g}={a}$
に帰着するが、この $A$ の誘導抗力部分（ $Q_{ij}$ だった部分)に多角形化行列の転置行列を左から、多角形化行列を右からかけたものに変更すると、なんと、多角形の状態で最適化計算ができるのだ！

つまりはこういうこと
$\begin{bmatrix} \begin{array}\\ &Q+Q^{T}& \\ \end{array} & \begin{array} -c_1&-b_1\\ \vdots&\vdots \\-c_n&-b_n \end{array} \\ \begin{array} -c_1&\cdots&-c_n \\ -b_1&\cdots&-b_n \end{array} & \begin{array} 0&0\\0&0 \end{array} \end{bmatrix}*\begin{bmatrix} g_1\\ \\\vdots\\ \\g_n \\\mu_1 \\\mu_2 \end{bmatrix}=\begin{bmatrix} 0\\ \\\vdots\\ \\0 \\1 \\\beta \end{bmatrix}$

となる逆行列問題の各行列に以下のように多角形化行列をかけてやる。mはセクションの総数であり、行列の大きさはグッと減っている（セクションの総数＋2の行数になる)
$\begin{bmatrix} \begin{array}\\ &POL^{T}*(Q+Q^{T})*POL& \\ \end{array} & \begin{array} -C_1&-B_1\\ \vdots&\vdots \\-C_m&-B_m \end{array} \\ \begin{array} -C_1&\cdots&-C_m \\ -B_1&\cdots&-B_m \end{array} & \begin{array} 0&0\\0&0 \end{array} \end{bmatrix}*\begin{bmatrix} g_{sec1}\\ \\\vdots\\ \\g_{secm} \\\mu_1 \\\mu_2 \end{bmatrix}=\begin{bmatrix} 0\\ \\\vdots\\ \\0 \\1 \\\beta \end{bmatrix}$

ここで
$C=(\begin{array}c_1&\cdots&c_n \end{array})*POL$ (揚力制約の行列に右から多角形化行列をかける）
$B=(\begin{array}b_1&\cdots&b_n \end{array})*POL$ (構造制約の行列に右から多角形化行列をかける）
である。

このようにしてラグランジュの未定乗数法で解くことで、簡単に多角形で誘導抵抗最小な循環分布が探索可能なのだ。

さて、構造制約を外して、多角形化した場合としなかった場合の誘導抗力の大きさの違いを調べてみた。
もちろん、多角形化しなければ誰もが知っている「楕円循環分布」となる。その結果がこちら（スパン34.6m 機速7.5m/s 揚力90kgf)

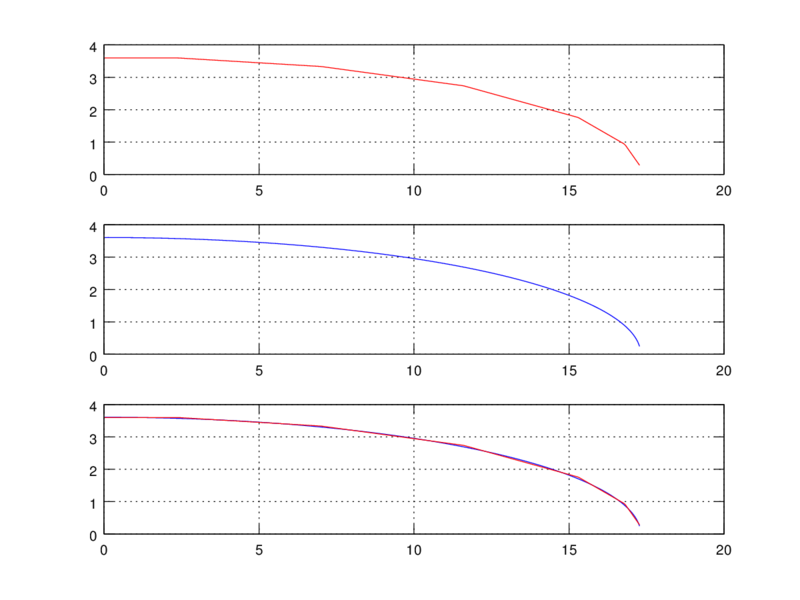
見て分かるとおり、上が多角形化した楕円循環、真ん中が多角形化しない楕円循環、一番下が重ねてみたグラフ、である。

このときの誘導抗力は
多角形化したものが、5.9667N
多角形化しないものが、5.9599N
その差、0.0068695N

という結果になった。多角形化して最適化すれば、多角形化しない楕円循環分布とほとんど変わらない値となる。これで楕円循環分布より作りやすいとくれば、ぜんぜん損はない。

実はTR797の改良の真骨頂は、工夫した構造制約のところにあるのだけれども、今回は多角形化の記事にした。
この多角形化行列、もっともっと応用すれば、設計作業（最適化作業)はもっと楽になる。なんせ、変数がグッと減るのだから。

*1:y-ysec1)/(ysec2-ysec1